Image Generative Model (Part 1): Generative Adversarial Networks

1. Generative Model vs Discriminative Model

“Generative” Models describes a class of statistical models that contrasts with Discriminative Models:

• Generative models can generate new data instances.
• Discriminative models discriminate between different kinds (label) of data instances.

More formally, given a set of data instances X and a set of labels Y:

• Generative models capture the joint probability $p(X,Y)$, or just $p(X)$ if there are no labels.
• Discriminative models capture the conditional probability $p(Y|X)$.

A generative model captures the distribution of the data, and generate new example base on that distribution, while a discriminative model tell how likely that a label(s) is to apply to the instance.

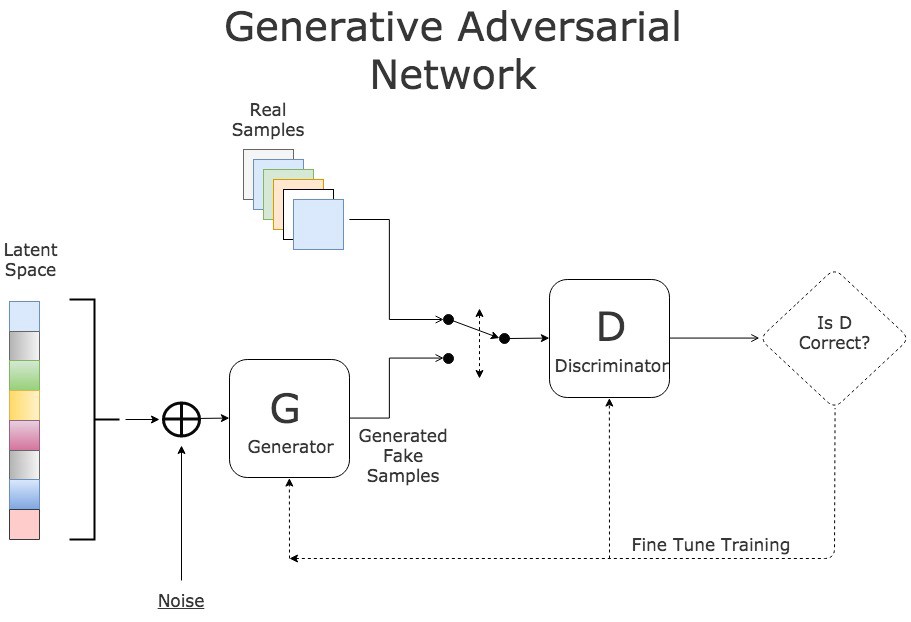
2. Generative Adversarial Networks (GANs)

A GAN has two parts:

• The generator learns to generate new instances and to fool the discriminator (negative training exmaples)
• The discriminator learns to distinguish the fake instances from the generator with the real instances from the training dataset and penalizes the generator for producing implausible results

2.1. Generator

The input of the generator is usually noise (e.g Gaussian Noise) and the output is the fake instances (e.g fake number from the MNIST dataset)

Because with one label (e.g number 0) the dataset have a lot of variety, so using noise to input to the generator will introduce randomness and variablity to the generated data, and the generator can learns to map the noise to the meaningful representations in the data distribution. The noise can also be seen as the latent representation of the data, which the generator tries to learn in an implicit manner.

self.generator = nn.Sequential(
  nn.Linear(in_features,256),
  nn.LeakyReLU(0.01),
  nn.Linear(256,512),
  nn.LeakyReLU(0.01),
  nn.Linear(512,1024),
  nn.LeakyReLU(0.01),
  nn.Linear(1024,out_features),
  nn.Tanh() # normalize output to [-1,1]
)

2.2. Discriminator

Discriminator tell us whether the instances is real (from data) or fake (from generator).

Discriminator act like a binary classification, which input a flatten image and output a value between 0 (fake) and 1(real).

self.discriminator = nn.Sequential(
  nn.Linear(in_features,1024),
  nn.LeakyReLU(0.01),
  nn.Linear(1024,512),
  nn.LeakyReLU(0.01),
  nn.Linear(512,256),
  nn.LeakyReLU(0.01),
  nn.Linear(256,1),
  nn.Sigmoid() # normalize output to [0,1]
)

2.3. Loss Function

Denote $x$ is the real image from the dataset, $z$ is the input noise to the generator, the Generator network is $G$ and the Discriminator is $D$. Then $G(z)$ will be the generated image from the Generator, $D(x)$ and $D(G(z))$ determined how “real” is the real image and the generated image, respectively.

• The discriminator is a binary classifier to distinguish if the input $x$ is real (from real data) or fake (from the generator). Typically, the discriminator outputs a scalar prediction 𝑜 ∈ R for input x, such as using a fully connected layer with hidden size 1, and then applies sigmoid function to obtain the predicted probability $D(x)=\frac{1}{1+e^{-o}}$. The discriminator is trained to minimized the cross-entropy loss, i.e.

\[\underset{D}{\min} \{-y \log D(x)-(1-y)\log(1-D(x))\}\]

• The goal of the generator is to fool the discriminator to classify $x’= 𝐺(z)$ as true data, i.e., we want $D(G(z)) ≈ 1$. In other words, for a given discriminator 𝐷, we update the parameters of the generator 𝐺 to maximize the crossentropy loss when 𝑦 = 0, i.e.,

\[\underset{G}{\max} \{-(1-y)\log (1-D(G(z))) \} = \underset{G}{\max} \{ -\log (1-D(G(z)))\}\]

• If the generator does a perfect job, then $D(x)’ \approx 1$, so the above loss is near 0, which results in the gradients that are too small to make good progress for the discriminator. So commonly, we minimize the following loss:

\[\min_{G} \{-y \log(D(G(z)))\} = \min_G \{-\log (D(G(z))) \}\]

• To sum up, $D$ and $G$ are playing a “minimax” game with the comprehensive objective function:

\[\min_{D} \max_{G} \{-E_{x \sim Data} [\log D(x)] - E_{z \sim Noise} [\log (1 - D(G(z)))] \}\]

Here are implementation in Pytorch:

### Train Discriminator: max log(D(x)) + log(1 - D(G(z)))
noise = torch.randn(batch_size, z_dim).to(device)
fake = gen(noise)
disc_real = disc(real).view(-1)
lossD_real = F.binary_cross_entropy(disc_real, torch.ones_like(disc_real))
disc_fake = disc(fake).view(-1)
lossD_fake = F.binary_cross_entropy(disc_fake, torch.zeros_like(disc_fake))
lossD = (lossD_real + lossD_fake) / 2
disc.zero_grad()
lossD.backward(retain_graph=True)
opt_disc.step()

### Train Generator: min log(1 - D(G(z))) <-> max log(D(G(z))
# where the second option of maximizing doesn't suffer from
# saturating gradients
output = disc(fake).view(-1)
lossG = F.binary_cross_entropy(output, torch.ones_like(output))
gen.zero_grad()
lossG.backward()
opt_gen.step()

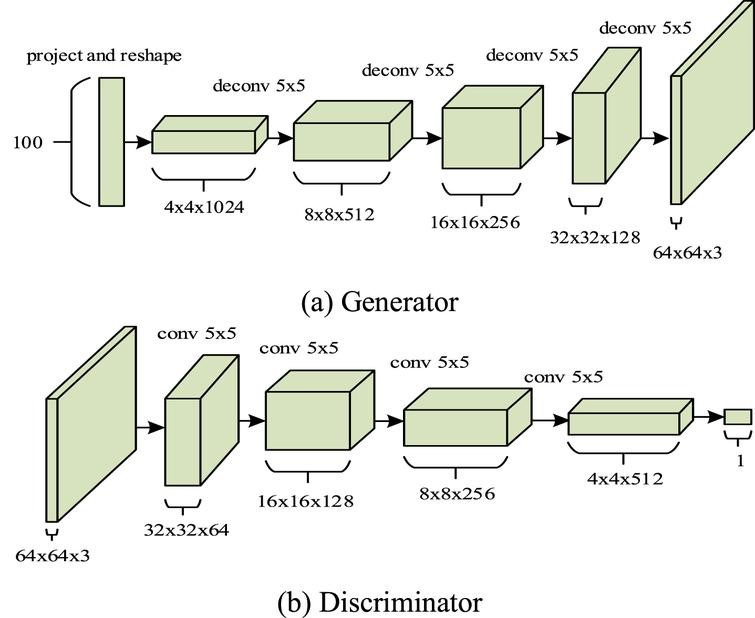
3. Deep Convolutional GAN (DCGAN)

DCGAN have similar objective as GAN, with a modification to the network architecture: replace fully connected network with CNN in both Generator and Discriminator.

Continued!