Transformer from Scratch
We will explore the power of the Transformer algorithm, the driving force behind the remarkable success of Large Language Models. Additionally, I will take you on a journey of building this algorithm from the ground up, providing you with a comprehensive understanding of its inner workings.
I. Key - Query - Value
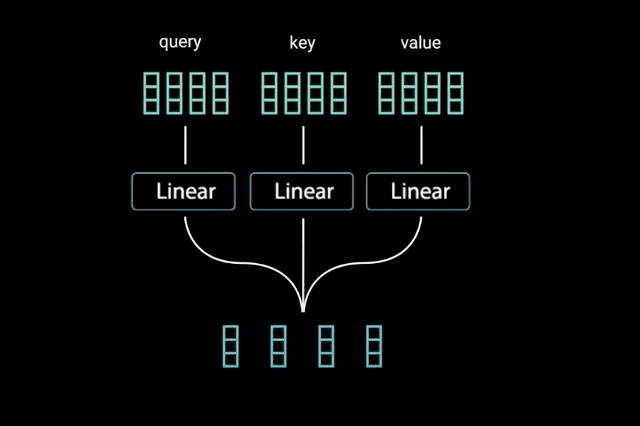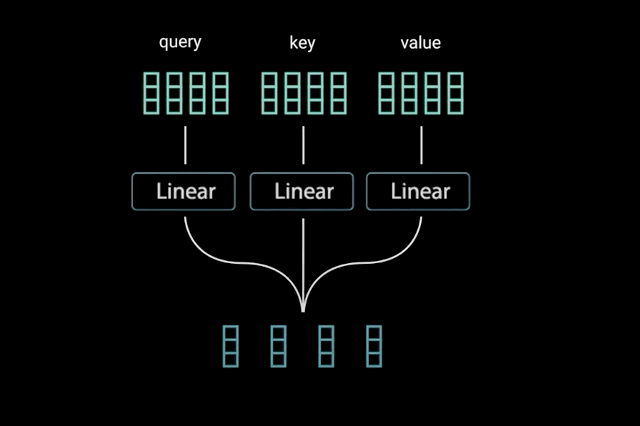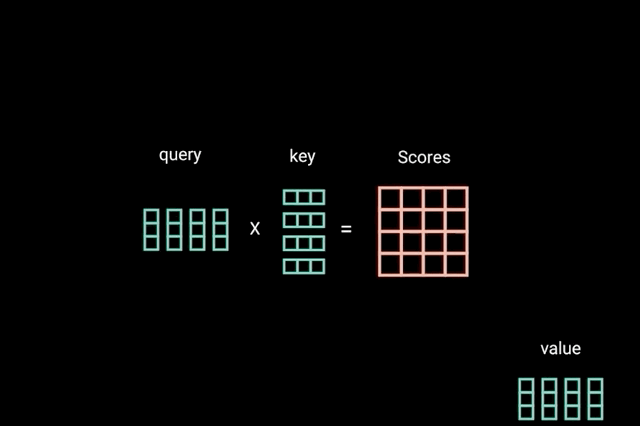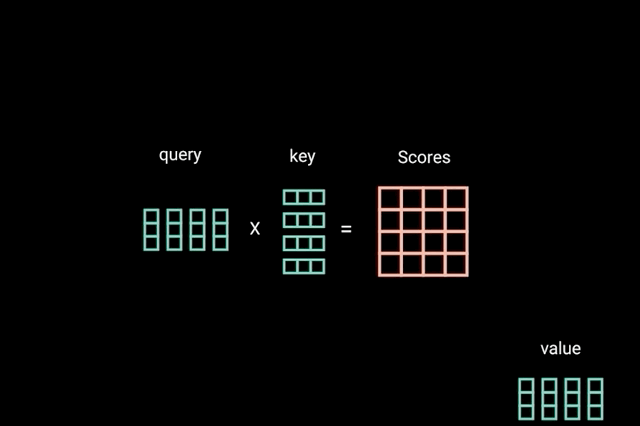
The key/value/query concept is analogous to retrieval systems.
For example, when you search for videos on Youtube, the search engine will map your query (text in the search bar) against a set of keys (video title, description, etc.) associated with candidate videos in their database, then present you the best matched videos (values).
II. Attention Mechanism
1. Attention
The attention operation can be thought of as a retrieval process as well.
\[\alpha(\mathbf{q}, \mathbf{k}_i) = \mathrm{softmax}(a(\mathbf{q}, \mathbf{k}_i)) = \frac{\exp(\mathbf{q}^\top \mathbf{k}_i / \sqrt{d})}{\sum_{j=1} \exp(\mathbf{q}^\top \mathbf{k}_j / \sqrt{d})}\]Denote by $\mathcal{D} \stackrel{\mathrm{def}}{=} {(\mathbf{k}_1, \mathbf{v}_1), \ldots (\mathbf{k}_m, \mathbf{v}_m)}$ a database of m tuples of keys and values. Moreover, denote by q a query. Then we can define the attention over $\mathcal{D}$ as
where $\alpha(\mathbf{q}, \mathbf{k}_i) \in \mathbb{R}$ (i=1,…,m) are scalar attention weights.
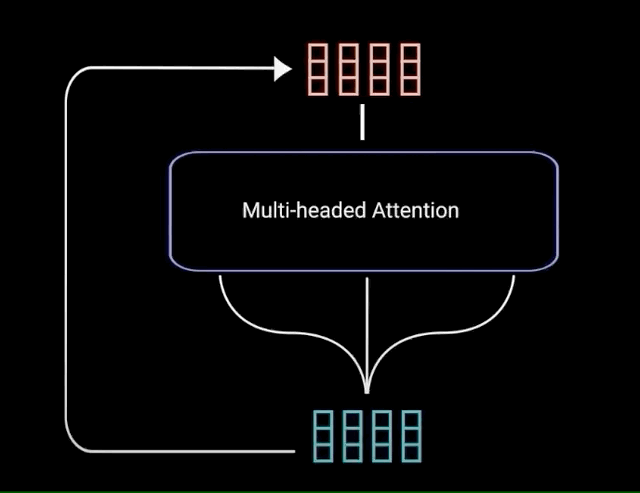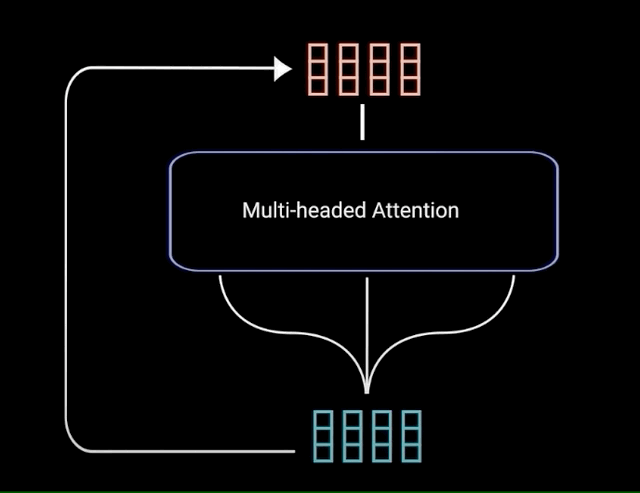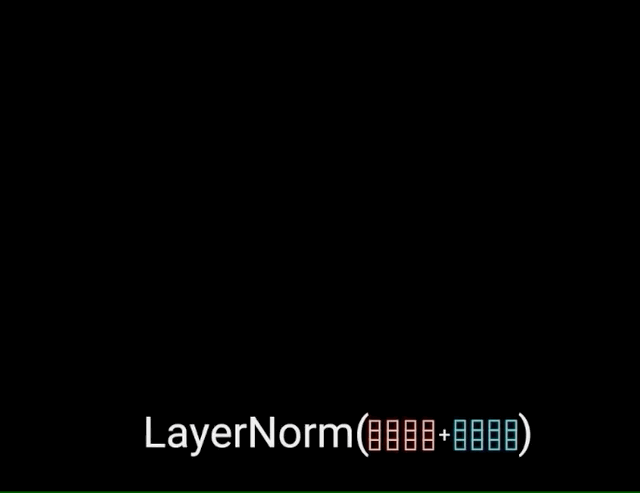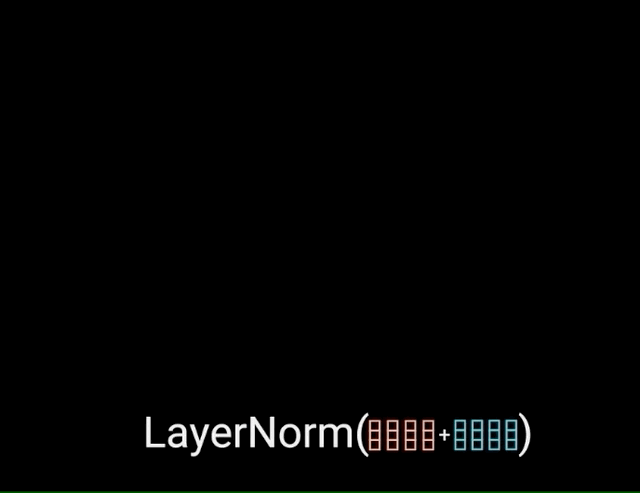
2. Multi-Head Attention
Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.
\[MultiHead(Q,K,V) = [head_{1},...,head_{h}]W^{O}\] \[\text{where } {head*{i}} = \text{Attention }(Q{W*{i}^{Q}},K{W*{i}^{K}},V{W*{i}^{V}})\]Where the projections are parameter matrices $W_{i}^{Q} ∈ R^{d_{model}×d_{k}} , W_{i}^{K} ∈ R^{d_{model}×d_{k}} , W_{i}^{V} ∈ R^{d_{model}×d_{v}}$ and $W^{O} ∈ R^{hd_{v}×d_{model}}$
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class MultiHeadAttention(nn.Module):
def __init__(self,embed_size,heads,bias=False):
super(MultiHeadAttention,self).__init__()
self.embed_size = embed_size
self.heads = heads
self.heads_dim = int(embed_size / heads)
self.keys = nn.Linear(embed_size,embed_size,bias=bias)
self.queries = nn.Linear(embed_size,embed_size,bias=bias)
self.values = nn.Linear(embed_size,embed_size,bias=bias)
self.fc = nn.Linear(embed_size,embed_size,bias=bias)
def forward(self,key,query,value,mask=None):
keys = self.keys(key).reshape(key.shape[0],key.shape[1],self.heads,self.heads_dim)
queries = self.queries(query).reshape(query.shape[0],query.shape[1],self.heads,self.heads_dim)
values = self.values(value).reshape(value.shape[0],value.shape[1],self.heads,self.heads_dim)
keys = keys / (self.embed_size)**(1/4)
queries = queries / (self.embed_size)**(1/4)
dot_product = torch.einsum('bkhd,bqhd->bhqk',keys,queries)
if mask is not None:
dot_product = dot_product.masked_fill(mask==0,float('-inf'))
scaled_product = torch.softmax(dot_product ,dim=3)
alpha = torch.einsum("bhqk,bvhd->bqhd",scaled_product,values)
out = self.fc(alpha.reshape(key.shape[0],key.shape[1],self.embed_size))
return out
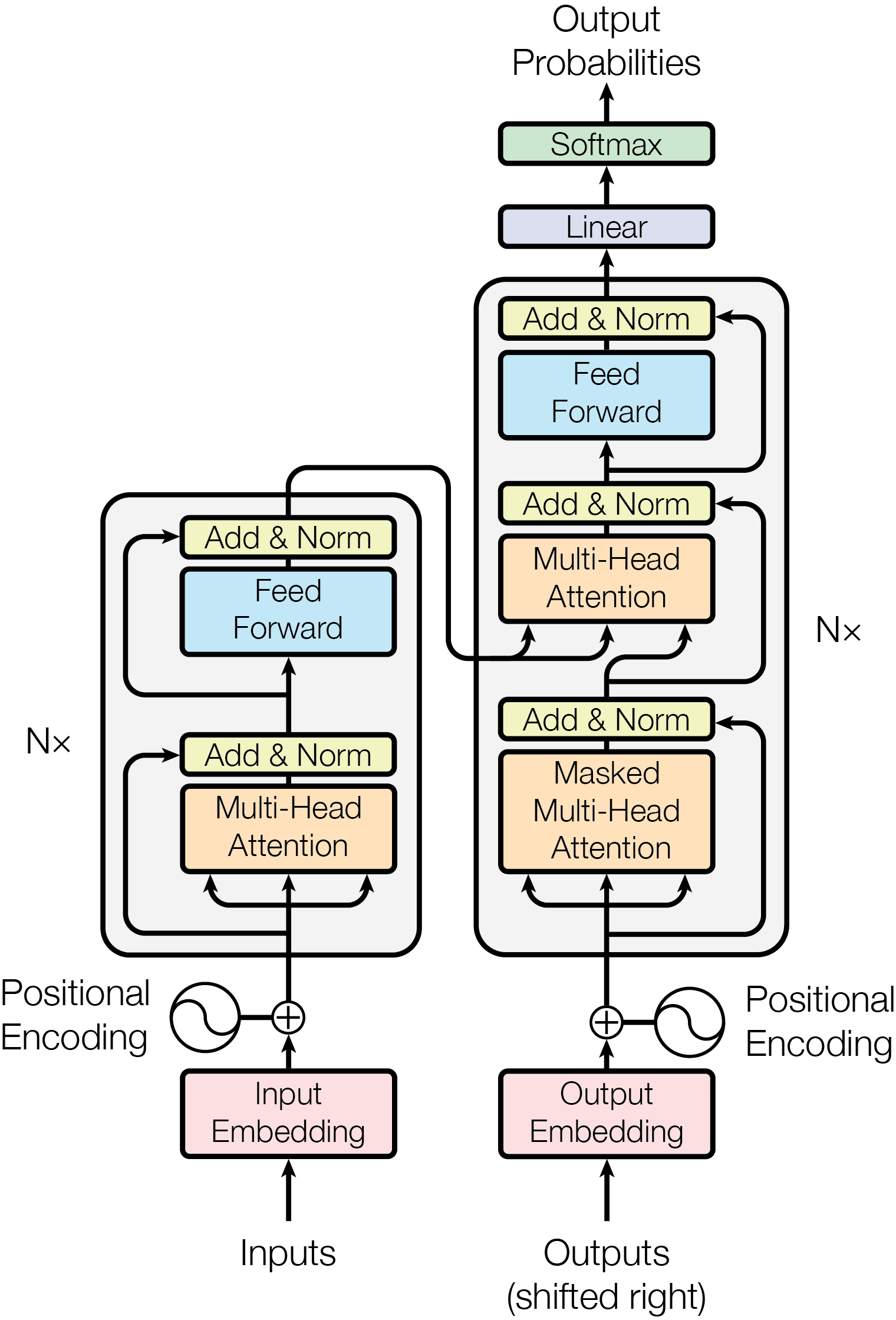
III. Encoder Decoder
Most competitive neural sequence transduction models have an encoder-decoder structure. Here, the encoder maps an input sequence of symbol representations $(x_{1}, …, x_{n})$ to a sequence of continuous representations $z = (z_{1}, …, z_{n})$. Given z, the decoder then generates an output sequence $(y_{1}, …, y_{m})$ of symbols one element at a time. At each step the model is auto-regressive, consuming the previously generated symbols as additional input when generating the next.
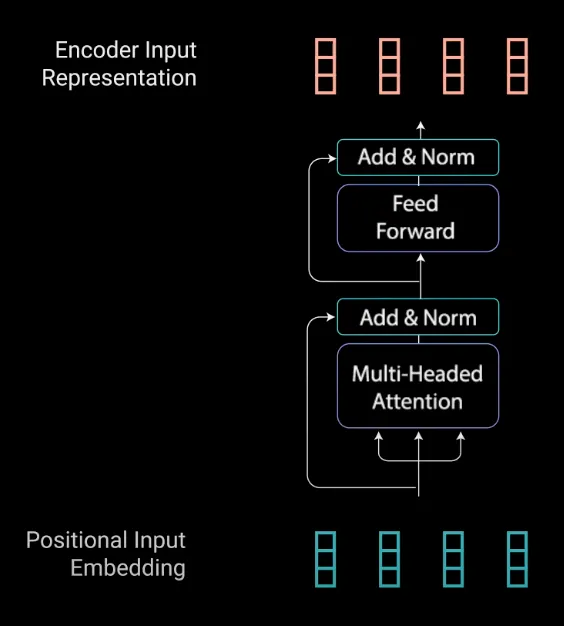
The Transformer follows this overall architecture using stacked self-attention and point-wise, fully connected layers for both the encoder and decoder
1. Positional Encoding
Positional encoding describes the location or position of an entity in a sequence so that each position is assigned a unique representation.
The positional encoding outputs X+P using a positional embedding matrix $\mathbf{P} \in \mathbb{R}^{n \times d}$ of the same shape, whose element on the $i^{th}$ row and the ${(2j)}^{th}$ or the ${(2j+1)}^{th}$ column is:
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class PositionalEncoding(nn.Module):
def __init__(self,num_hiddens,dropout = 0.5,max_len=1000):
super(PositionalEncoding,self).__init__()
PE = torch.zeros((1,max_len,num_hiddens))
self.dropout = nn.Dropout(dropout)
position = torch.arange(0,max_len,dtype=torch.float32).reshape(-1,1) \
/ torch.pow(10000,torch.arange(0,num_hiddens,2,dtype=torch.float32) / num_hiddens)
PE[:,:,0::2] = torch.sin(position)
PE[:,:,1::2] = torch.cos(position)
self.register_buffer('PE',PE)
def forward(self,x):
x = x + self.PE[:,:x.shape[1],:]
return self.dropout(x)
2. The Residual Connections, Layer Normalization, and Feed Forward Network
The multi-headed attention output vector is added to the original positional input embedding. This is called a residual connection. The output of the residual connection goes through a layer normalization.
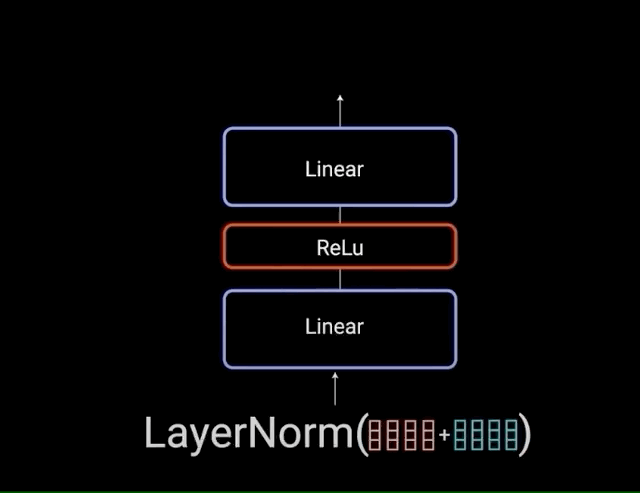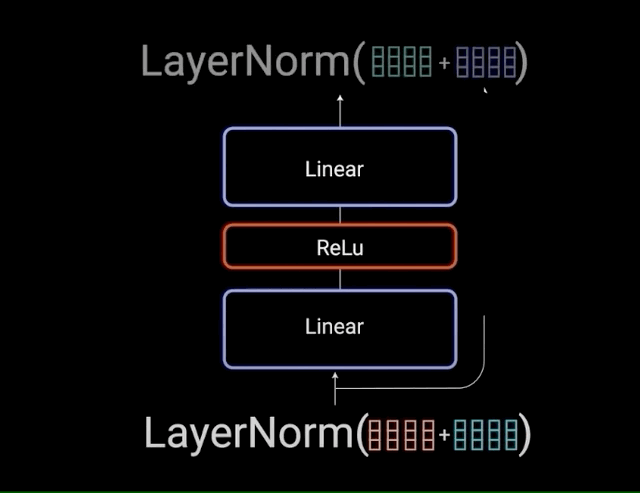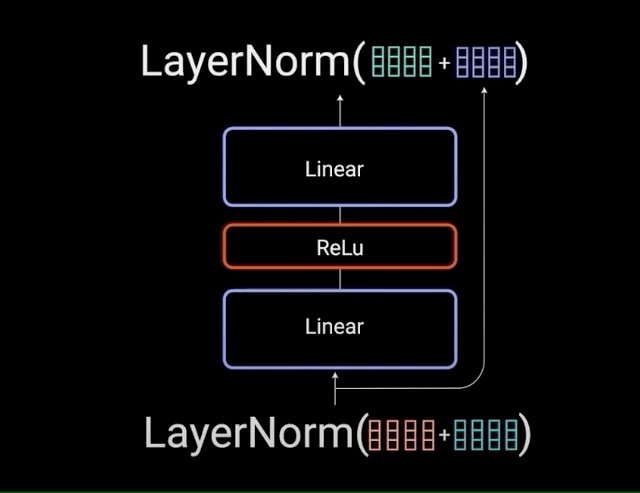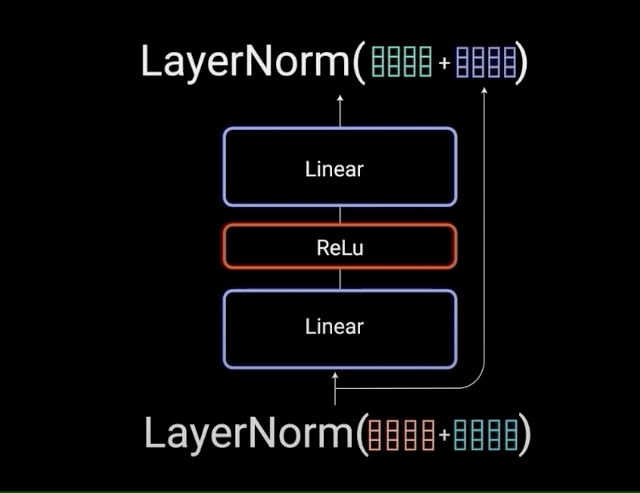
Each of the layers in our encoder and decoder contains a fully connected feed-forward network, which is applied to each position separately and identically. This consists of two linear transformations with a ReLU activation in between.
\[FFN(x) = max(0,x{W}_{1} + b_{1}){W}_{2} + b_{2}\]The residual connections help the network train, by allowing gradients to flow through the networks directly. The layer normalizations are used to stabilize the network which results in substantially reducing the training time necessary. The pointwise feedforward layer is used to project the attention outputs potentially giving it a richer representation.
3.Masking
Decoders First multi-headed attention layer operates slightly differently. Since the decoder is autoregressive and generates the sequence word by word, you need to prevent it from conditioning to future tokens
4.Encoder
The Encoders layers job is to map all input sequences into an abstract continuous representation that holds the learned information for that entire sequence. It contains 2 sub-modules, multi-headed attention, followed by a fully connected network. There are also residual connections around each of the two sublayers followed by a layer normalization.
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class EncoderBlock(nn.Module):
def __init__(self,embed_size,heads,bias=False):
super(EncoderBlock,self).__init__()
self.attention = MultiHeadAttention(embed_size,heads,bias)
self.layer_norm1 = nn.LayerNorm(embed_size)
self.layer_norm2 = nn.LayerNorm(embed_size)
self.feed_forward = nn.Sequential(
nn.Linear(embed_size,4*embed_size),
nn.GELU(),
nn.Linear(4*embed_size,embed_size)
)
def forward(self,key,query,value,mask=None):
attention = self.attention(key,query,value,mask)
out = self.layer_norm1(key + attention)
out_ffw = self.feed_forward(out)
out = self.layer_norm2(out + out_ffw)
return out
class Encoder(nn.Module):
def __init__(self,vocab_size,embed_size,heads,num_layers,max_len,dropout,bias=False):
super(Encoder,self).__init__()
self.embed = nn.Embedding(vocab_size,embed_size)
self.position_embed = PositionalEncoding(embed_size,max_len=max_len,dropout=dropout)
self.encoder_layers = nn.ModuleList(
[
EncoderBlock(embed_size,heads,bias)
for _ in range(num_layers)
]
)
self.dropout = nn.Dropout(dropout)
def forward(self,x,mask):
x_embed = self.embed(x)
x_embed = self.position_embed(x_embed)
out = self.dropout(x_embed)
for layer in self.encoder_layers:
out = layer(out,out,out,mask)
return out
5. Decoder
The decoder’s job is to generate text sequences. The decoder has a similar sub-layer as the encoder. it has two multi-headed attention layers, a pointwise feed-forward layer, and residual connections, and layer normalization after each sub-layer. These sub-layers behave similarly to the layers in the encoder but each multi-headed attention layer has a different job. The decoder is capped off with a linear layer that acts as a classifier, and a softmax to get the word probabilities.
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class DecoderBlock(nn.Module):
def __init__(self,embed_size,heads,bias=False):
super(DecoderBlock,self).__init__()
self.encoder_block = EncoderBlock(embed_size,heads,bias)
self.attention = MultiHeadAttention(embed_size,heads,bias)
self.layer_norm = nn.LayerNorm(embed_size)
self.dropout = nn.Dropout()
def forward(self,x,enc_value,enc_key,src_mask,target_mask):
out = self.layer_norm(x + self.attention(x,x,x,src_mask))
out = self.dropout(out)
out = self.encoder_block(key=enc_key,value=enc_value,query=out,mask=target_mask)
return out
class Decoder(nn.Module):
def __init__(self,vocab_size,embed_size,heads,num_layers,max_len,dropout,bias=False):
super(Decoder,self).__init__()
self.embed = nn.Embedding(vocab_size,embed_size)
self.position_embed = PositionalEncoding(embed_size,max_len=max_len,dropout=dropout)
self.decoder_layer = nn.ModuleList(
[
DecoderBlock(embed_size,heads,bias)
for _ in range(num_layers)
]
)
self.dropout = nn.Dropout(dropout)
self.fc = nn.Linear(embed_size,vocab_size)
def forward(self,x,encoder_out,src_mask,target_mask):
x_embed = self.embed(x)
x_embed = self.position_embed(x_embed)
out = self.dropout(x_embed)
for layer in self.decoder_layer:
out = layer(out,encoder_out,encoder_out,src_mask,target_mask)
out = self.fc(out)
return out
IV. Conclusion
(To be continued)